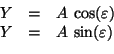This article describes the deviation of the formulas used in GLWaves
for calculations concerning the polarisation ellipse.
We consider a wave superposed of two linearely polarized waves, one in X
direction, the other one in Y direction. They have 90 in between.
These are defined by
in between.
These are defined by
 |
(1) |
Both waves have their own amplitude and phase offset. The instantaneous angle
is written  here for simplicity. A real wave has
here for simplicity. A real wave has
 .
If we superpose both waves we will get an elliptically polarized wave. The E
vector describes an ellipse. Silently we assume the x and y coordinates being
proportional to the x and y component of the field strength vector,
respectively.
.
If we superpose both waves we will get an elliptically polarized wave. The E
vector describes an ellipse. Silently we assume the x and y coordinates being
proportional to the x and y component of the field strength vector,
respectively.
Figure:
The polarisation ellipse with all its parameters used in this article
 |
This ellipse is centered at the origin. Its major axis has the length 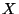 , its
minor axis the lenth
, its
minor axis the lenth  . The major axis' inclination to the
. The major axis' inclination to the 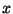 axis is
denoted by
axis is
denoted by 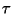 .
The rectangle described by the amplitudes of the E field components has a
hypotenuse angle called
.
The rectangle described by the amplitudes of the E field components has a
hypotenuse angle called  , the rectangle streched by the ellipse
axes has an angle known as
, the rectangle streched by the ellipse
axes has an angle known as
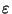 .
.
Handedness 
The angle  is obviously given by
is obviously given by
 |
(2) |
Given are the amplitudes  ,
,  and the phase offsets
and the phase offsets  and
and
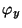 . We search the inclination angle
. We search the inclination angle 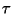 and the ellipse axes
lengths
and the ellipse axes
lengths 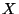 and
and  .
Therefore we define the length of the compound E vector
.
Therefore we define the length of the compound E vector
 |
(3) |
The maxium of the length appears in the the major axis' direction. The
derivation of the length1 by the angle  has to be zero.
has to be zero.
![$\displaystyle \frac{\partial l^2}{\partial\xi} = - E_x^2\,\sin\left[2\,(\xi + \varphi_x)\right] - E_y^2\,\sin\left[2\,(\xi + \varphi_y)\right] \stackrel{!}{=} 0$](img19.png) |
(4) |
This supplies the angle
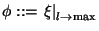 when the superposed waves point to the
major axis
when the superposed waves point to the
major axis
 |
(5) |
where
 , the phase difference.
, the phase difference.
Equations ![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) with
with
 2 give the x and y coordinate of the
major axis
2 give the x and y coordinate of the
major axis
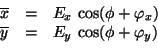 |
(6) |
whereas
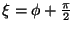 results in the coordinates of the minor
axis
results in the coordinates of the minor
axis
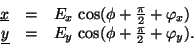 |
(7) |
The length of the axes is then given by
 |
(8) |
Inclination 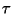
The angle 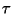 specifying the inclination of the ellipse now is easily
determined by
specifying the inclination of the ellipse now is easily
determined by
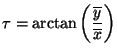 |
(9) |
Ellipticity
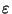
The ellipticity
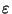 results to
results to
 |
(10) |
This section is a treatise on the derivation of the wave parameters  ,
,
 ,
,  and
and 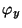 when the ellipse parameters
when the ellipse parameters  ,
, 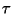 or
or
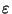 are given.
are given.
 is determined by the component amplitudes
is determined by the component amplitudes  and
and  (see eq.
(
(see eq.
(![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) )) so we have to reversely calculate both amplitudes from the
given
)) so we have to reversely calculate both amplitudes from the
given  . Therefore we need a second equation. We can take one of these
. Therefore we need a second equation. We can take one of these
-
 const.
const.
-
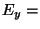 const.
const.
-
 const.
const.
The most meaningful is variant ![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) . First the diagonal of the current
rectangle is determined as
. First the diagonal of the current
rectangle is determined as
 |
(11) |
what we directly use in the equations for the new amplitudes
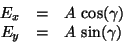 |
(12) |
(remember the unit circle and the trigonometric functions). The phase offsets
don't depend on  .
.
Finally we recalculate 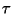 and
and
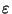 since they change with
since they change with  .
The calculation is given in subsections
.
The calculation is given in subsections ![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) and
and ![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) ,
respectively.
,
respectively.
The polarisation ellipse can be described as a horizontal ellipse in a
rotated coordinate system (rotated by the inclination angle 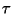 ).
The coordinate transformation will be derived now.
).
The coordinate transformation will be derived now.
Figure:
The blue coordinate system is rotated by the angle 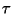 relative to the black coordinate system.
relative to the black coordinate system.
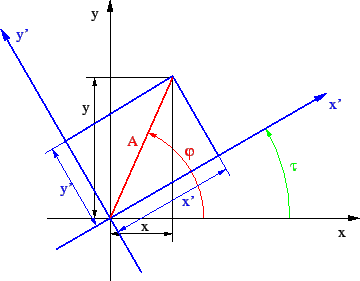 |
The coordinates in the base coordinate system 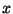 and
and  are rendered as
are rendered as
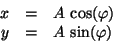 |
(13) |
In the rotated coordinate system  the coordinates are given by
the coordinates are given by
 |
(14) |
which can be simplified to the coordinate transformation
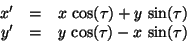 |
(15) |
The backward transformation
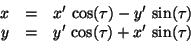 |
(16) |
Component maxima
In the rotated coordinate system the ellipse is given by
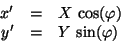 |
(17) |
In the base coordinate system this equals to
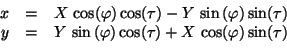 |
(18) |
where the angle 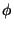 refers to the rotated coordinate system.
refers to the rotated coordinate system.
The components' amplitudes appear when these coordinates have their maximum.
The angle 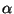 relative to the major axis points to the amplitude of
relative to the major axis points to the amplitude of
 ,
, 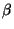 denotes the amplitude of
denotes the amplitude of  .
.
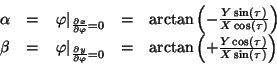 |
(19) |
Using that result the field strength components are given by
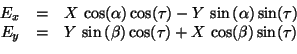 |
(20) |
When the x component of the elliptically polarized electromagnetic wave takes
its maximum (this is at
 ), the y component's value must
be (compare with eq. (
), the y component's value must
be (compare with eq. (![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) )
) )
)
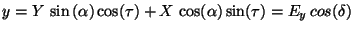 |
(21) |
with
 being the phase difference between
being the phase difference between 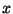 and
and  . Solving this equation for
. Solving this equation for 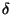 finishes the problem.
finishes the problem.
 |
(22) |
Attention: be careful with this
 . Little inaccuracies and the
granularity of floating point calculations can lead to an argument
. Little inaccuracies and the
granularity of floating point calculations can lead to an argument
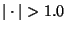 raising a floating point exception.
raising a floating point exception.
Since changing the field strength components also affects the handedness
 , it has to be calculated as described in section
, it has to be calculated as described in section ![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) .
.
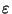 doesn't change because the ellipse is rotated as is.
doesn't change because the ellipse is rotated as is.
The ellipticity
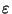 is determined by the ellipse axes
is determined by the ellipse axes 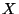 and
and  so
we have to reversely calculate both from the given
so
we have to reversely calculate both from the given
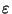 . Therefore we
again need a second equation.
. Therefore we
again need a second equation.
-
 const.
const.
-
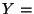 const.
const.
-
 const.
const.
Item number ![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) gives the best result. The diagonal of the
ellipticity rectangle derives to
gives the best result. The diagonal of the
ellipticity rectangle derives to
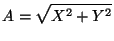 |
(23) |
The new axes lengths thus become
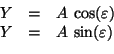 |
(24) |
(recall unit circle and trigonometric functions). The values  ,
,  ,
,
 ,
, 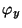 and
and  (
(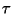 is held constant when
is held constant when
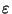 is changed) are given by the equations derived in section
is changed) are given by the equations derived in section
![[*]](https://glwaves.sourceforge.net/usr/share/latex2html/icons/crossref.png) .
.
Footnotes
- ... length1
- Here we differentiate the square of the
length
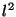 . This is allowed since the length is surely greater than zero
and the square is a monotone transformation on the positive axis. It
simplifies the calculation enormously.
. This is allowed since the length is surely greater than zero
and the square is a monotone transformation on the positive axis. It
simplifies the calculation enormously.
- ...#tex2html_wrap_inline502#�2
- we simply use the absolute
values instead of the vectors here
Johann Glaser Johann.Glaser@gmx.at
![]() in between.
These are defined by
in between.
These are defined by
![]() here for simplicity. A real wave has
here for simplicity. A real wave has
![]() .
If we superpose both waves we will get an elliptically polarized wave. The E
vector describes an ellipse. Silently we assume the x and y coordinates being
proportional to the x and y component of the field strength vector,
respectively.
.
If we superpose both waves we will get an elliptically polarized wave. The E
vector describes an ellipse. Silently we assume the x and y coordinates being
proportional to the x and y component of the field strength vector,
respectively.
![]() , its
minor axis the lenth
, its
minor axis the lenth ![]() . The major axis' inclination to the
. The major axis' inclination to the ![]() axis is
denoted by
axis is
denoted by ![]() .
The rectangle described by the amplitudes of the E field components has a
hypotenuse angle called
.
The rectangle described by the amplitudes of the E field components has a
hypotenuse angle called ![]() , the rectangle streched by the ellipse
axes has an angle known as
, the rectangle streched by the ellipse
axes has an angle known as
![]() .
.
![$\displaystyle \frac{\partial l^2}{\partial\xi} = - E_x^2\,\sin\left[2\,(\xi + \varphi_x)\right] - E_y^2\,\sin\left[2\,(\xi + \varphi_y)\right] \stackrel{!}{=} 0$](img19.png)

![]() with
with
![]() 2 give the x and y coordinate of the
major axis
2 give the x and y coordinate of the
major axis
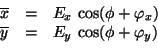
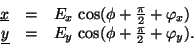

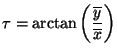

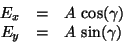
![]() and
and
![]() since they change with
since they change with ![]() .
The calculation is given in subsections
.
The calculation is given in subsections ![]() and
and ![]() ,
respectively.
,
respectively.
![]() and
and ![]() are rendered as
are rendered as
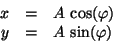

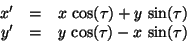
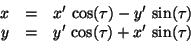
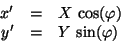
![]() relative to the major axis points to the amplitude of
relative to the major axis points to the amplitude of
![]() ,
, ![]() denotes the amplitude of
denotes the amplitude of ![]() .
.
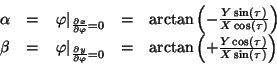
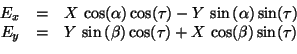

![]() , it has to be calculated as described in section
, it has to be calculated as described in section ![]() .
.
![]() doesn't change because the ellipse is rotated as is.
doesn't change because the ellipse is rotated as is.